18世紀にイギリスの聖職者であったトーマス・ベイズによって生み出されたのがベイズの定理です。
そして、ベイズの定理の考え方を重視する立場はベイズ主義(ベイジリアン)と呼ばれ、
ベイズ主義にもとづく統計学をベイズ統計学といいます。
ベイズ統計学の考え方が新しい考え方である2つの理由
結果と原因どちらに着目するか
皆さんがよく学校で習う確率は、ある原因からある結果がおきる確率です。
一方、ベイズ統計学で扱う確率はある結果からある原因がおきる確率です。
厚生労働省の生命表によると、平成17年に行われた調査における85歳までの死亡率は約10%です。
では、死亡者の死因は何でしょうか?がんで死亡してしまう確率は何でしょうか?
ベイズ統計学ではある結果がおき、その結果をもたらした原因について考えます。
原因がおきる確率を求めるための手段がベイズの定理です。
主観性と客観性
ベイズ統計学では、
「この方法なら7割方成功する!」
「この勉強法なら99%志望校に合格する!」
そんな主観的な、経験則的な場合を扱うことができます。
経験則的な確率が、学問として存在していいのでしょうか?
そういう訳で、「主観性」の点からベイズ統計学は長らく批判の対象でした。
証明できない確率を扱うベイズ統計学を学問として認めるのは難しいですよね。
主観確率を確かなものにするための考え方にベイズ更新があります。
ベイズの定理
条件つき確率とは、AがおきたときBがおきる確率です。
ex. 買い物に行ってリンゴを買ったとき、そのリンゴが腐っている確率
以降、原因をA、結果をBとします。
条件つき確率P(結果B|原因A)
\[P(結果B|原因A)=\frac{P(原因A\cap 結果B) }{P(原因A)}\tag{1}\]
ベイズの定理P(原因A|結果B)
\[P(原因A|結果B)=P(原因A)\times \frac{ P(結果B|原因A) }{P(結果B)}\tag{2}\]
ポイントは事前確率or事後確率です。
事前確率P(原因A)は、ある結果がおきる前の原因Aがおこる確率です。
では結果がおきた後に、次原因Aがおきる確率はどうなるでしょう?
壺から球を取り出して戻す問題で例を考えます。
赤と白の球が入っている壺から赤球を出す確率を求めます。
ここで、キン肉マンが球を取り出す場合、
キン肉マンは力が強すぎるため、一定確率で球が割れてしまいます。
割れた球はゴミ箱に捨てます。
この場合、赤球の出る確率は変化します。
ベイズの定理では、このような事後の変化を組み込ませた確率を扱うことができます。
「成長する確率」を扱うことができる定理がベイズの定理という認識で大丈夫です。
そして、このように事後に変化が伴う確率を事後確率といいます。
ベイズ更新
経験は日々の積み重ねで得られるものです。
ベイズの定理もまた繰り返し、積み重ねることで真の確率に近づきます。
このように、繰り返し、確率を更新していくことで数学的に正しいとする考え方がベイズ更新です。
ベイズ更新の考え方のメリットは主に2つです。
- 未知の確率を求められる
- 確率の精度を上げられる
天気予報が的中する確率を1、つまり100%的中するとします。
1日目の的中率は70%であったのでそれをもとにベイズの定理で確率を更新する。
2日目は75%で更新、3日目は79%で更新と同じ要領で続けていく。
そして、10000日目くらいには77%くらいに収束します。
ベイズ更新を利用する際に、最初に設定する確率は何でもいいです。
まず、未知の確率を適当に設定して、統計を取り始めます。
あとは、確率をコツコツと更新するだけで確率の精度を上がっていきます。
それだけで、未知の確率を真の確率に限りなく近づけることができます。
ベイズ統計学の考え方は人間の経験や学習とよく似ていることがわかります。
1人の経験では信用できないが、100000人から得た経験なら信用できるとし、データの数で「客観性」を補っています。
近年では、ベイズ更新の考え方と相性の良い分野として、AI(人工知能)、ビッグデータが注目されています。
具体的な利用例
病気の診断
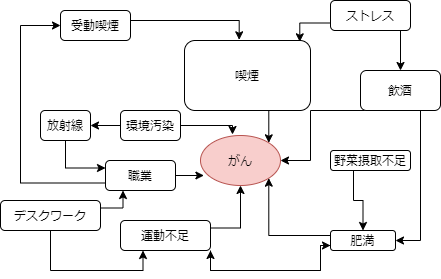
上の図はベイジリアンネットやベイジリアンネットワークと呼ばれ、
複雑な因果関係のある事象の分析に用いられます。
確率で分岐されたネットワークから、複雑な因果を読み解き、最適解を求めます。
それだけでなく、要素から要素に移るときの確率は更新されていき、
精度がどんどん上がっていきます。
以上の点からも、ベイジリアンネットの考え方はAI開発の基礎となっています。
近年、ベイジリアンネットがいち早く応用された分野が医療です。
例えば、以下の症状が出ている患者がいると仮定します。
- のどが「ゼーゼー、ヒューヒュー」いう喘鳴
- 空咳
- 発作性の激しい咳や痰
ベイジリアンネットを用いることで、これらの症状から病名が「喘息(ぜんそく)」である確率が高いことが推測できます。
複雑な因果関係から最適解を求めることがベイズ統計ではできるのです。
現在のところ、ベイジリアンネットは医師の診断を裏付ける、
あるいは、誤診を減らすためのサポートという形で利用されています。
迷惑メール
メールを評価して、振り分けてくれるプログラムにフィルターというものがあります。
迷惑メールフィルターにはベイズ更新の仕組みが用いられています。
仕組み
迷惑メールフィルターでは、ベイズの定理を用いて迷惑メールである確率を求め、
その結果から迷惑メールフォルダに入れるかを判定します。
もしフィルターが誤判定をしたとしても、多くの迷惑メールは人間の目で見極められるものが多いので、人間なら見分けることができます。
そして、人間が正しい判定を行うことで、迷惑メールフィルターのプログラムが学習し、
ベイズ更新の考え方に基づき事後確率を求めます。
それにより、次同じようなメールが来たとき、そのメールを迷惑メールフォルダに入れることができるのです。
また、迷惑メールは絶えず来るので、事後確率の精度は上がり、迷惑メールフィルターの性能はどんどん向上していきます。


コメント