今回のテーマはギャンブルと確率についてです。
パチンコ、パチスロ、競馬をはじめとするギャンブルが身近な存在となっている現代、
多くのギャンブラーがそれぞれの理論と熱をもって、ギャンブル生活を送っているはずです。
このように、、、
まあ…未熟ゆえ取り逃しましたがね…!
賭博破戒録カイジ 2話より
しかし…もう大丈夫…!わかるんですっ…!
次は勝てる…
絶対にね…!
見えているっ!
オレは負けないっ…!
漫画の世界では、負けても逆転するようなドキドキさせる展開がほとんどです。
しかし、現実世界では大逆転という展開はめったに起こりません。
そこで、少しでも勝ちを増やし負けを減らすことで、コツコツと収支をプラスにしたいのです。
そして、そのために様々な理論や心得がうまれています。
ギャンブルに興味のある方なら、
「負けを取り戻すのはNG」
「勝ったらすぐやめる」
といった心得を知っているのではないでしょうか。
では、それらの心得について確率を用いて考えてみましょう。
大数の法則とは
大数の法則は、スイスの数学者ヤコブ・ベルヌーイ(1654~1705)によって証明されました。
大数の法則:
ある確率Pで起こるそれぞれが独立した事象に関して、試行の回数を増やすほど、実際にその事象が起こる確率はPに近づくという法則
そして、次章で大数の法則とギャンブルがどのように密接に関わっているのか考えていきましょう!
独立:
それぞれの事象が互いに影響をおよぼすことなく、互いに無関係であるということ。
独立した事象
サイコロを3回投げ、3回とも1が出る確率P
\[P=\frac{1}{6}\times\frac{1}{6}\times\frac{1}{6} \]
何回サイコロを振っても、それぞれの回で1が出る確率は常に1/6となる。
独立でない事象
赤球4個、青球2個の入った袋から1つずつ球を取り出していき、3回目に青が出る確率P
\[P=\frac{4}{6}\times\frac{3}{5}\times\frac{2}{4}+ \frac{4}{6}\times\frac{2}{5}\times\frac{1}{4}+\frac{2}{6}\times\frac{4}{5}\times\frac{1}{4} \]
取り出した結果、次に取りだせる球の数が減ってしまうため、
次に球を取り出すときの確率に影響を与えてしまう。
よって、単純に確率の積だけで求めることはできない。
独立でない事象などの動的な確率を考えるため、
ベイズ統計学はAIやデータサイエンスの場で積極的に利用されている学問です。
もしよろしければ、参考にしてください!
ギャンブルをすればするほど損をする理由
大数の法則より
皆さんも、人生ゲームやすごろくをやったことがあるはずです。
そのとき、「なんで、こんな1ばっかり出るの?」「6全然でないよ~」と感じたことがありませんか?
ゲームでは試行の数が少ないため、出る目のばらつきがでてしまいます。
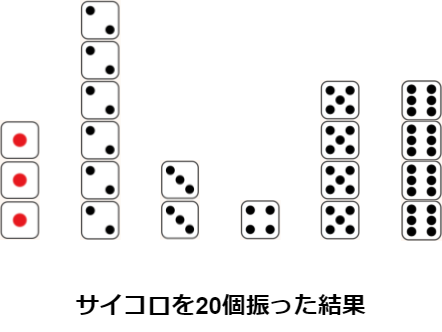
しかし、サイコロを1000回振ってみると出る目のばらつきは気にならなくなります。
このように、試行の数を増やすことで偏りが少なくなるという法則が大数の法則です。
ちなみに、サイコロの目の出方は一般的に独立しているため、大数の法則が利用できます。

ギャンブルの性質より
ギャンブルは胴元が有利なように、還元率がおよそ決まっています。
還元率:
使ったお金と戻ってくるお金の割合
\[還元率=\frac{戻ってくるお金}{使ったお金}\]
ここで、還元率の高い順からギャンブルの種類を並べてみました。
| ギャンブルの種類 | 還元率(およそ) |
| オンラインカジノ | 95% |
| パチンコ・スロット | 85% |
| 競馬 | 75% |
| 競艇 | 75% |
| 競輪 | 75% |
| オートレース | 70% |
| 宝くじ | 45% |
まとめ
大数の法則より、やればやるほど論理上の確率(還元率)に近づき、
ギャンブルの性質より、還元率は胴元が有利なように設定されています。
よって、ギャンブルはやればやるほど大数の法則よりもともと設定されていた還元率に近づいていきます。
負けてしまったら、続けたところで大数の法則よりマイナスは広がる一方。
→「負けを取り戻すのはNG」
勝っても続けてしまったら、大数の法則よりそのうち還元率に近づきプラスはなくなる。
→「勝ったらすぐやめる」



コメント